note_2 特征

未分类
2.6k 词

用于后续手写python进行转换参考

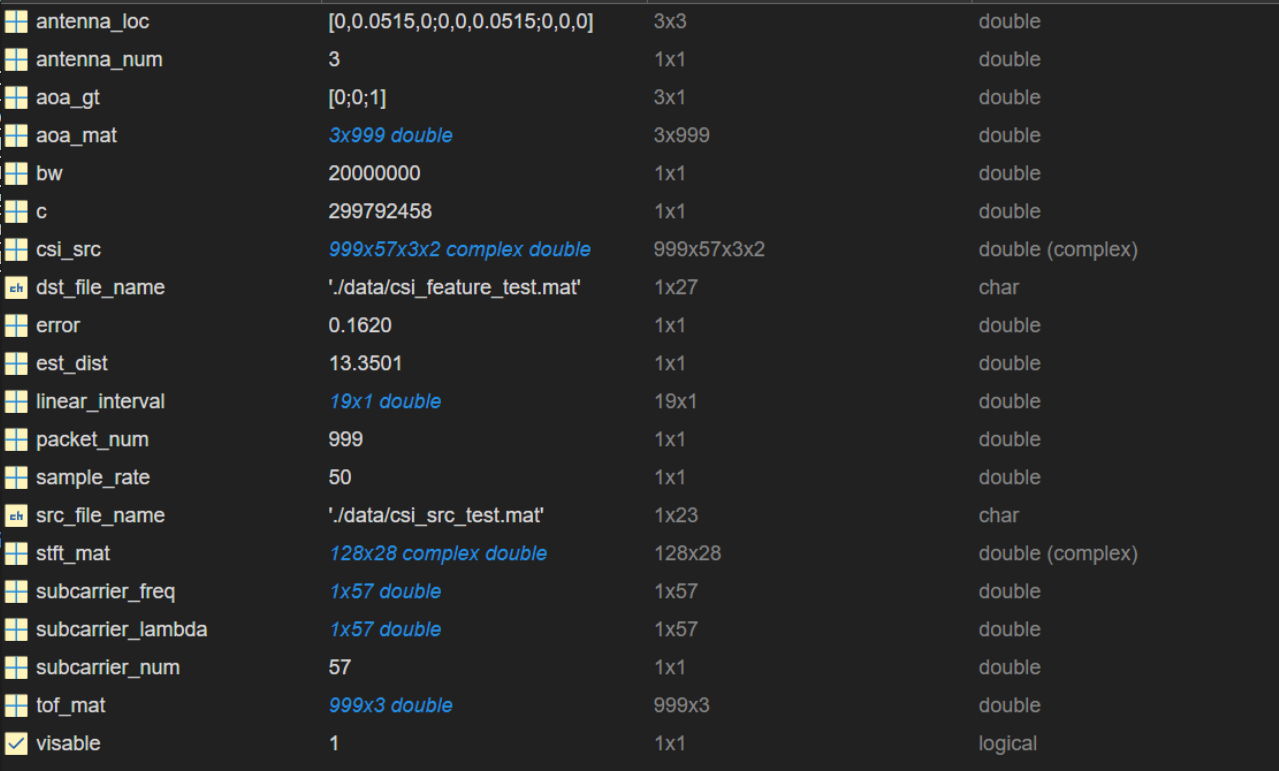
alt text

main

  1. 计算子载波波长

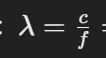
alt text

  1. 天线排列

linspace(5.8153e9, 5.8347e9, 57);创建一个等间隔的频率数组。
linspace函数用于生成一个在指定区间内均匀分布的数值序列，起始频率5.8153GHz，终止频率5.8347GHz，生成的间隔数值57。

num2str 将数值转换为字符串

  1. 计算偏差
  • 计算AoA估计

aoa_mat = naive_aoa(csi_src, antenna_loc, zeros(3, 1)); zeros(3,1)适用于RCO（射频链路偏移）的零向量，在这个例子里，RCO被假设为0

aoa_gt = [0; 0; 1]; 给定的地面真实AoA向量，假设实际AoA沿着z的单位向量

error = mean(acos(aoa_gt' * aoa_mat)); 里面先计算点积，得到余弦相似度，acos(cos(theta))就得到theta，两个向量之间的夹角，取平均，得到所有估计值的平均角度误差

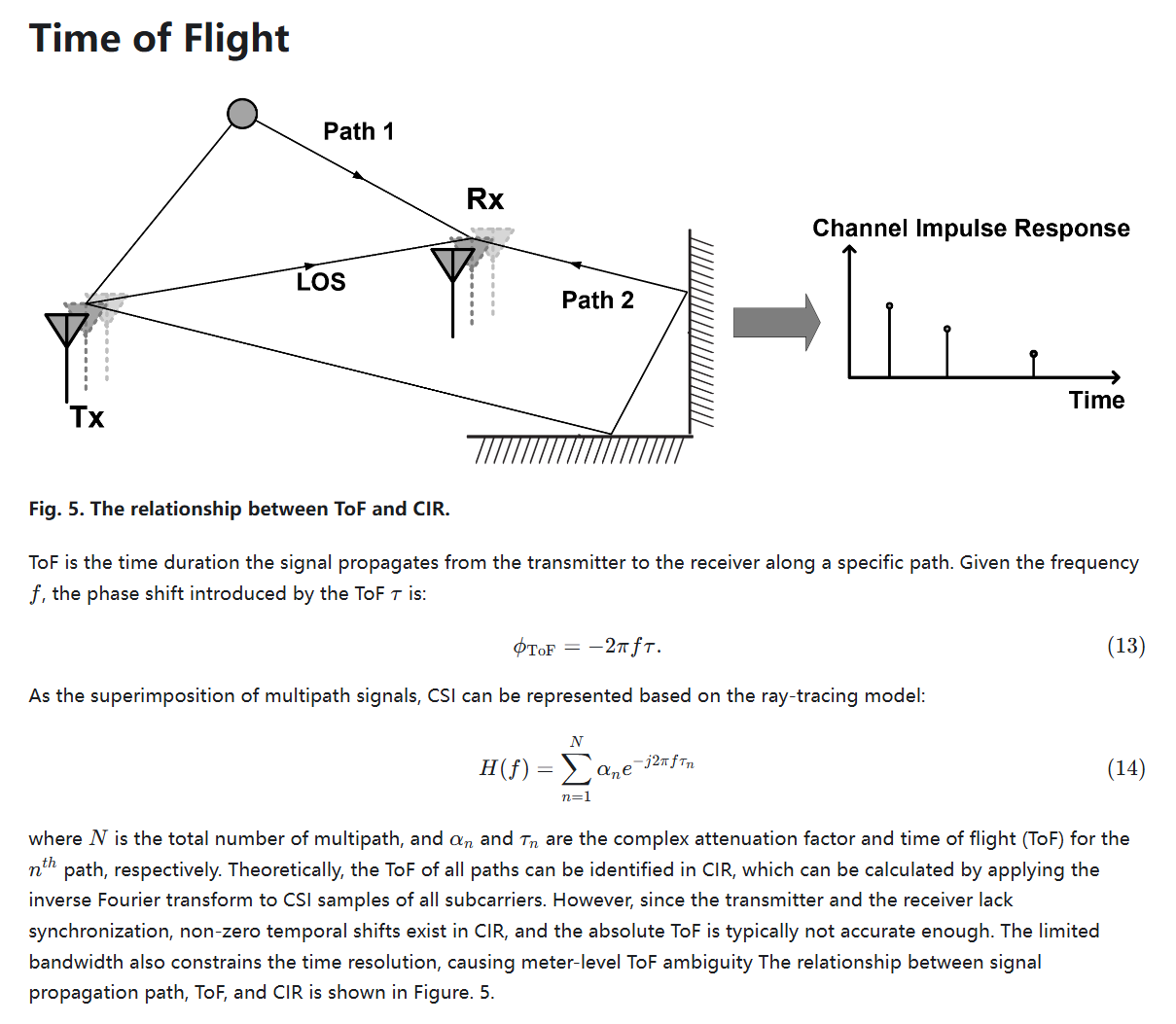
alt text

TOF

概念

TOF

alt text

alt text

英文翻译中文

alt text

代码注解

输入:

  • csidata csi数据 [T S A L]，T为时间点，S为子载波，A为天线数量，L是CSI数据的其他维度
    输出：
  • tof_mat 粗略的飞行时间估计结果 [T A] 表示每个时间点和每个天线的飞行时间估计
  1. 计算IFFT点数

ifft_point = power(2, ceil(log2(subcarrier_num)));

将点数调整到最接近的2的幂次方，以优化IFFT的计算。快速傅里叶变换（FFT）和逆快速傅里叶变换（IFFT）算法的计算复杂度对于2的幂次方的点数具有最佳性能。计算效率会随着点数的增加而提高，特别是在处理大规模数据时。

  1. 计算CIR（信道脉冲响应）

cir_sequence = ifft(csi_data, ifft_point, 2);在第二个维度（子载波维度）进行IFFT。

先对第四维度求均值，然后squeeze去除维度为1的单一维度。旨在操作去除第4维（L维）的影响，通过对该维度求均值来得到每个时间点和天线的平均CIR。

  1. 只考虑一半的IFFT点数，因为信道的时域通常是对称的

  2. 查找CIR峰值

[~, peak_indices] = max(half_sequence, [], 2); % [T 1 A]第二维度（子载波维度）上计算最大值。
第一个返回：每个时间点和每个天线在指定维度的最大值
第二个返回：最大值的位置索引

然后squeeze去除维度为1的单一维度。

  1. 计算飞行时间

用于确定信号从发送端到接收端所花费的时间，计算到达时间与发射时间之间的差异。

(峰值位置 * 子载波数) / (IFFT点数 * dw)

最后，再 *c 就是距离

AoA

从 CSI 数据中估计到达角

概念

物理背景：天线阵列的相位差。为了得到theta

alt text

alt text

alt text

alt text

代码注解

输入:

  • csidata 用于角度估计的csi数据 [T S A L]
  • antenna_loc 以第一个天线为参考的天线位置排列 [3 A]
  • est_rco 估计的射频链路便宜（RCO）[A 1]
    输出：
  • aoa_mat 角度估计的结果 [3 T]
  1. 相位解包（消除相位跳跃）

消除相位跳跃（unwrap phase）是信号处理中的一个重要步骤，用于处理由于相位周期性而导致的相位不连续问题。在处理相位信息时，由于相位值的周期性（通常是-2𝜋到2π），相位在不同周期之间可能会出现不连续的跳跃。相位跳跃会导致相位数据的分析和计算结果出现错误。

常见消除相位的方法：

  • 相位解包，标准方法，通过加上或减去适当的2𝜋整数倍。
  • 数学处理，例如线性插值和平滑算法。
  1. 计算天线差向量及其长度
  • 计算天线差向量

ant_diff = antenna_loc(:, 2:end) - antenna_loc(:, 1); % [3 A-1]

第一个天线与其他天线之间的差异向量 = 选择从第二个天线到最后一个天线的所有位置向量 - 选择的第一个天线的位置向量

  • 计算天线差向量长度

ant_diff_length = vecnorm(ant_diff); % [1 A-1]

计算每个差向量的欧几里得范数（向量长度），vecnorm会沿列计算

  • 规范化天线差向量

对每个差向量进行归一化，转换为单位向量

  1. 计算相位差

alt text

alt text

这里，沿第二维（子载波维度）展开相位，得到一个连续的相位差值

alt text

  1. 计算cos(theta)

alt text

permute(ant_diff_length, [3 1 2]) 调整维度使得能与phase_diff进行广播运算 [1 1 A-1 1]，第三维度默认1

cos_mat_mean = squeeze(mean(cos_mat, [2 4])); % [T A-1]

  • 在第二维（子载波）和第四维（链路）上取平均值，得到数据包和天线对的平均cos(theta)
  • 去除维度为1的单一维度，简化矩阵大小。不会改变结果，仅仅改变矩阵的形状，去掉无意义的单一矩阵。
  1. 解线性方程

\在matlab中，是求解线性方程组，求解最小二乘法。使用线性方程组解 AoA 估计值。

  1. 结果归一化并处理奇异性问题

  • 找出无效维度。先计算矩阵在第二维度上的总和，若维度对应的天线对之间差异为0，则无法进行有效的角度估计。

  • 找出有效维度。

setdiff(A, B) 是 MATLAB 中的一个函数，用于计算集合 A 中那些不在集合 B 中的元素

  • 对无效维度进行处理。

    • 计算有效维度上角度估计结果的平方和。
      sum(aoa_mat_sol(valid_dim, :) .^ 2, 1) sum(...,1)对每列（每个样本）的平方和进行求和
    • 计算无效维度的估计值
      sqrt((1-有效维度平方和)/无效维度数量)
    • 填充无效维度
      repmat(..., 1, length(invalid_dim))

  • 结果更新

STFT 短时傅里叶变换

概念

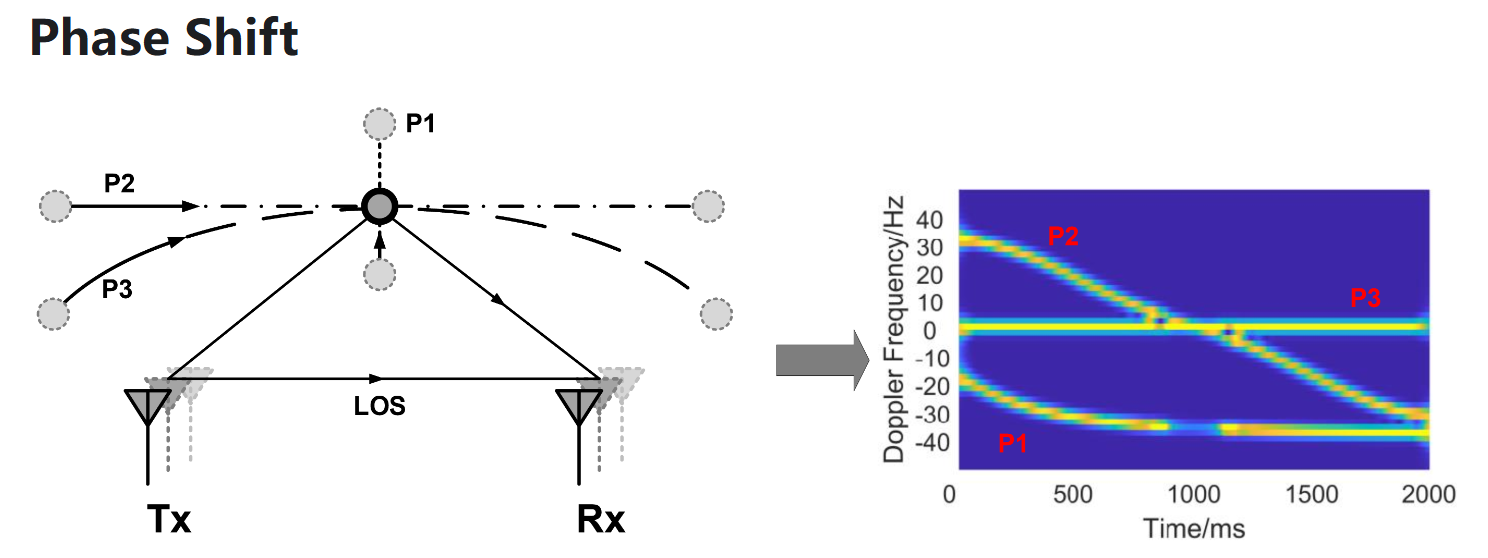
alt text

短时傅里叶变换（STFT）是一种用于分析信号在时间和频率域上变化的方法。它的主要作用是将时间域信号转换为时间-频率域。

sample_rate 采样率，指定了信号的采样频率。

alt text

代码注解

输入:

  • csidata 用于生成STFT频谱的csi数据 [T S A L]
  • sample_rate 确定时域和频域的分辨率
    输出：
  • stft_mat 生成的STFT频谱 [sample_rate/2 T]
  1. 共轭相乘

csi_data .* conj(csi_data) 对每个时间点、子载波、天线和其他，计算共轭相乘，得到功率谱密度。

再对第二、三、四维度取均值，得到具有时间密度的功率谱密度图。可以将[T S A L]维度减小到[T]

  1. 计算STFT

  2. 可视化

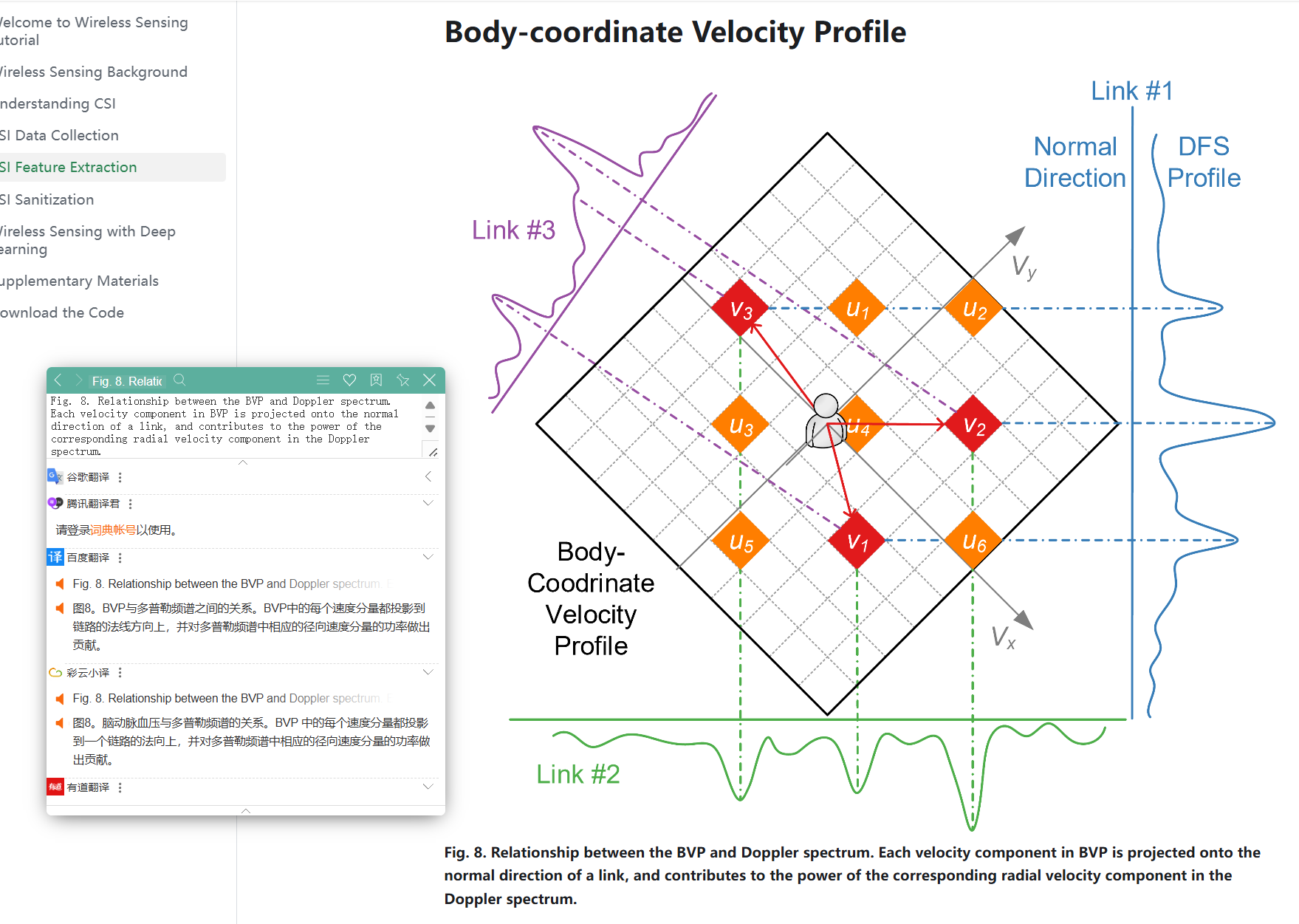
BVP体坐标速度剖面

概念

alt text

alt text

alt text

alt text

留言